1. 队列相关

一、实现一个队列函数，保持最多两个任务同时进行，多余的任务进行排队，待某一个任务完成后再按照顺序执行下一个任务

例如

addTrack(1000, 1)
addTrack(200, 2)
addTrack(500, 3)
addTrack(900, 4)
// 输出如下结果
// 200ms  后输出 2
// 700ms  后输出 3
// 1000ms 后输出 1
// 1600ms 后输出 4

实现

let doing = 0 // 正在请求的数量
const wating = [] // 等待请求的数组
let time = Date.now()

function call(element) {
  setTimeout(() => {
    console.log(element.value, Date.now() - time)
    // 正在请求-1
    doing--
    // 如果还有数组长度，取先进来的执行
    if (wating.length > 0) {
      doing++
      call(wating[0])
      // 记得从等待的数组删除
      wating.shift()
    }
  }, element.time);
}
function addTrack(time, value) {
  const element = {
    time,
    value
  }
  // 小于2直接执行
  if (doing < 2) {
    doing++
    call(element)
  } else {
    wating.push(element)
  }
}
addTrack(1000, 1)
addTrack(200, 2)
addTrack(500, 3)
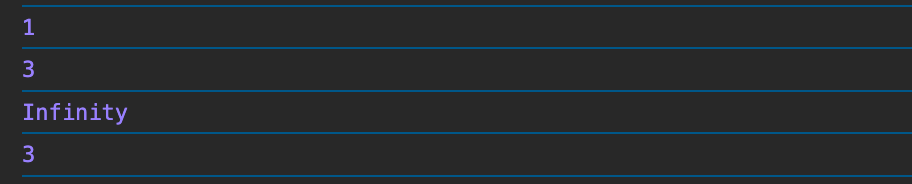
addTrack(900, 4)

运行结果

二、为了充分发挥GPU算力，需要尽可能多的将任务交给GPU执行，现在有一个任务数组，数组元素表示在这1秒内新增的任务个数且每秒都有新增任务，假设GPU最多一次执行n个任务，一次执行耗时1秒，在保证GPU不空闲情况下，最少需要多长时间执行完成

例如

输入：
3, [1, 2, 3, 4, 5]
输出：
6

输入：
4, [5, 4, 1, 1, 1]
输出：
5

实现

function minExecutionTime(maxExec, tasks) {
  let remaining = 0, time = 0
  for (let task of tasks) {
    if (task + remaining > maxExec) {
      remaining = task + remaining - maxExec;
    } else {
      remaining = 0;
    }
    time += 1;
  }
  while (remaining > 0) {
    remaining -= maxExec;
    time += 1;
  }
  return time
}
console.log(minExecutionTime(3, [1, 2, 3, 4, 5]));
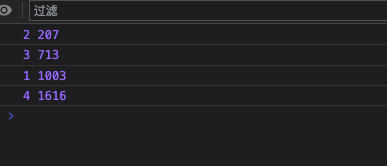
console.log(minExecutionTime(4, [5, 4, 1, 1, 1]));

运行结果

2.排序相关

一、输入一个数字数组，输出其全部递增元素数组

例如

increment([1, 5, 4, 7, 8, 4])
increment([5, 4, 3, 7, 8])
increment([5, 4, 3, 2, 1])
// 输出如下结果
// [[1,5], [4,7,8]]
// [[3,7,8]]
// []

实现

function increment(arrIn) {
    let incrementTemp = [] // 缓存比较结果
    const arrOut = [] // 返回结果
    arrIn.forEach((el, index) => {
        // 第一项直接push，不需要比较
        if (index === 0) {
            incrementTemp.push(el)
            return
        }
        const len = incrementTemp.length
        const lastEl = incrementTemp[len - 1]
        // 判断是否比前一个大
        if (el > lastEl) {
            incrementTemp.push(el)
        } else {
            // 判断是否多于两个，是则为递增数列
            if (len > 1) {
                // 不能直接arrOut.push(incrementTemp)，incrementTemp会被后续清空
                arrOut.push([...incrementTemp])
            }
            // 将值的作为下一次比较
            incrementTemp = [el]
        }
    });
    // 循环完毕还需要将incrementTemp放入
    if (incrementTemp.length > 1) {
        arrOut.push([...incrementTemp])
    }
    console.log(JSON.stringify(arrOut));
    return arrOut
}

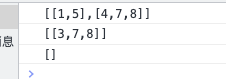
运行结果

二、蛇形矩阵是由1开始的自然数依次排列成的一个矩阵上三角形。

例如

当输入5时，应该输出的三角形为：
1 3 6 10 15
2 5 9 14
4 8 13
7 12
11
当输入4时，应该输出的三角形为：
1 3 6 10
2 5 9
4 8
7

实现

// 观察数字填入规律可知
// 行为递减，列为递增
// 比如输入4，则为
// [0,0] [1,0] [0,1] [2,0] [1,1] [0,2] [3,0] [2,1] [1,2] [0,3]
function func(value) {
  const arr = [] // 矩阵存放
  let n = 1 // 递增值
  for (let i = 0; i < value; i++) {
    for (let j = 0; j <= i; j++) {
      const left = i - j
      const right = j
      if (arr[left]) {
        arr[left][right] = n++
      } else {
        arr[left] = [n++]
      }
    }
  }
  arr.forEach(v => {
    console.log(v.join(' '))
  })
}

运行结果

3.链表相关

一、将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转

例如

输入：
{1,2,3,4,5},2,4
返回值：
{1,4,3,2,5}

实现

class HeadNode {
  value = 0
  next = null
  constructor(value, next) {
    this.value = value
    this.next = next
  }
}

/**
 * 打印链表内容
 */
function logHeadNode(headNode) {
  let log = []
  cur = headNode
  while (cur) {
    log.push(cur.value)
    cur = cur.next
  }
  console.log(log.join(','))
}

let head = new HeadNode(0, null)
let headNode = head

for (let i = 1; i < 5; i++) {
  let node = new HeadNode(i, null)
  head.next = node
  head = node
}

logHeadNode(headNode)

/**
 * 转化方法
 */
function transform(headNode, m, n) {
  let start = null, end = null, cur = headNode
  // 找到两个要反转的前后节点
  for (let i = 1; i <= n; i++) {
    if (i === m - 1) {
      start = cur
    }
    cur = cur.next
  }
  end = cur
  // 如果不是第一个位置
  if (m > 1) {
    let pre = null
    cur = start.next
    while (cur !== end) {
      let tmp = cur.next
      cur.next = pre
      pre = cur
      cur = tmp
    }
    start.next.next = end
    start.next = pre
  } else {
    let pre = headNode
    cur = headNode.next
    while (cur !== end) {
      let tmp = cur.next
      cur.next = pre
      pre = cur
      cur = tmp
    }
    headNode.next = end
    headNode = pre
  }
  return headNode
}

const headNode2 = transform(headNode, 2, 4)
logHeadNode(headNode2)

运行结果

4.滑动窗口

一、给定一个矩阵，包含N*M个整数，和一个包含K个整数的数组。现在要求在这个矩阵中找一个宽度最小的子矩阵，要求子矩阵包含数组中所有的整数

例如

输入：
[[1, 2, 3],
[3, 5, 6]], [3, 6]
返回值：
1
输入：
[[1, 2, 3],
[3, 5, 6]], [1, 6]
返回值：
3
输入：
[[1, 0, 1, 4],
[0, 0, 7, 8],
[1, 0, 11, 12],
[0, 0, 15, 16]], [1, 0, 1, 0, 1, 0]
返回值：
3

实现

function minSubmatrixWidth(matrix, nums) {
  const row = matrix.length, col = matrix[0].length;
  let minWidth = Infinity;
  // 从第一列开始滑动
  for (let i = 0; i < col; i++) {
    // 拷贝一份nums用于计算
    const numsCopy = [...nums];
    // 第二列以当前列开始
    for (let j = i; j < col; j++) {
      // 循环nums找到出现的数字进行删除
      for (let k = 0; k < row; k++) {
        const num = matrix[k][j];
        const index = numsCopy.indexOf(num);
        if (index !== -1) {
          numsCopy.splice(index, 1);
        }
        // 如果nums长度为0，说明全部包含了num，跳出行遍历
        if (numsCopy.length === 0) {
          minWidth = Math.min(minWidth, j - i + 1);
          // 宽度为1，肯定是最小，直接返回1即可
          if (minWidth === 1) {
            return 1
          }
          break
        }
      }
      // 如果nums长度为0，说明全部包含了，跳出这次滑动
      if (numsCopy.length === 0) {
        break
      }
    }
  }
  return minWidth
}

// 计算最小宽度的子矩阵
console.log(minSubmatrixWidth([
  [1, 2, 3],
  [3, 5, 6]
], [3, 6]));
console.log(minSubmatrixWidth([
  [1, 2, 3],
  [3, 5, 6]
], [1, 6]));
console.log(minSubmatrixWidth([
  [1, 2, 3],
  [3, 5, 6]
], [4]));
console.log(minSubmatrixWidth([
  [1, 0, 1, 4],
  [0, 0, 7, 8],
  [1, 0, 11, 12],
  [0, 0, 15, 16]
], [1, 0, 1, 0, 1, 0]));

运行结果